Wolfram最適化WOLFRAM言語の
コアとなる部分

設計のモデル化,解決,分析
Wolframの最適化は,最適な設計を見付けたり制約条件内で最高の決定をしたりするためのツールの包括セットを提供します.これらのツールは高度に自動化された機械学習や統計の機能およびその場で計算可能な組込みデータ等と完璧に統合されています.
最適化モデリング
数学関数,不等式,包含関係を目的関数や制約条件を使ってモデル化します.コンパクトで高レベルなモデルをベクトル変数,ベクトル不等式,幾何学領域によって自然な形で定義します.データ,グラフ,その他のオブジェクトからプログラムを使って再利用可能なモデルを構築します.
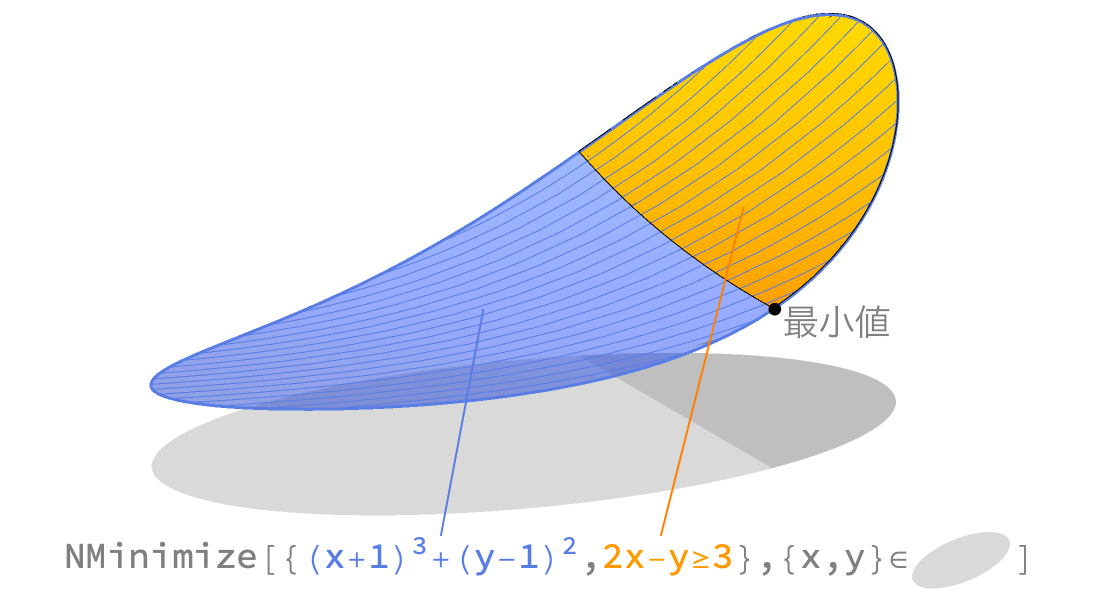
線形最適化と凸最適化
大規模な凸最適化問題を大域的で高速かつ信頼性があるメソッドで解きます.凸最適化には線形最適化,二次最適化,二次錐最適化,半定値最適化,錐最適化等の重要なクラスが含まれます.
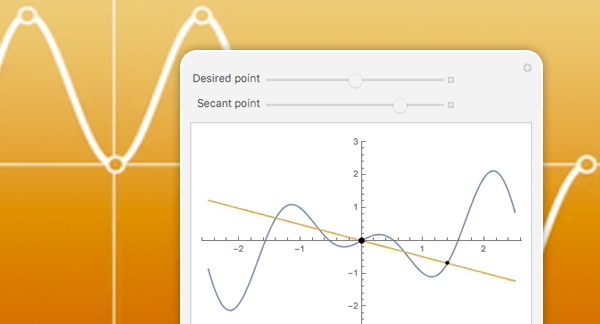
局所的最適化
制約条件付きまたは制約条件なしの最適化問題について,局所的な最適値を求めます.局所的なメソッドは高速かつスケーラブルで,それだけで十分なこともしばしばありますし,より高度なメソッドの構築に使われることもあります.擬似ニュートン法,内点法,導関数の計算や効率化のためのコンパイル等から自動選択されたメソッドを使って解を求めます.
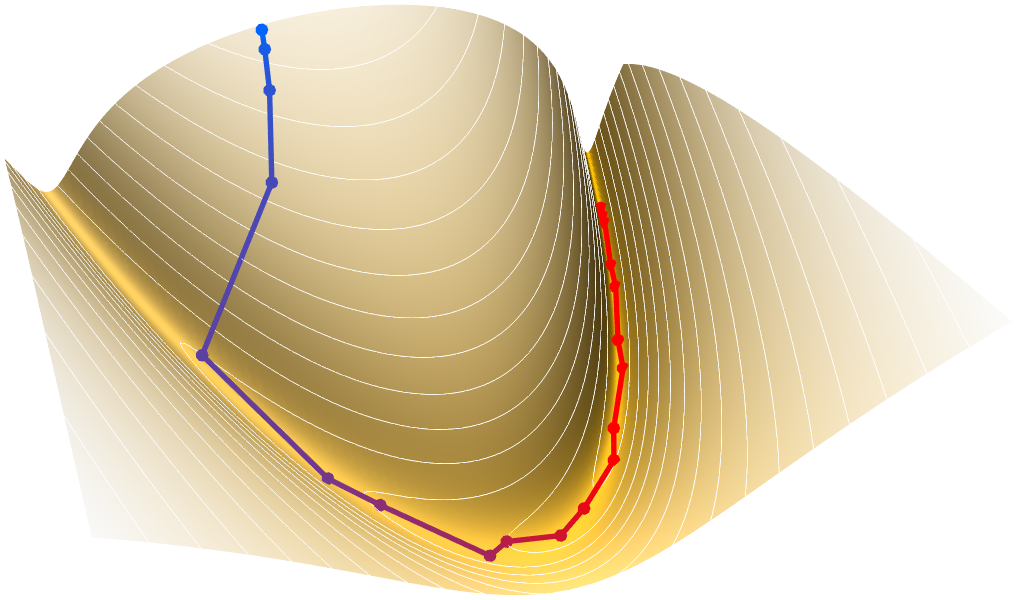
大域的最適化
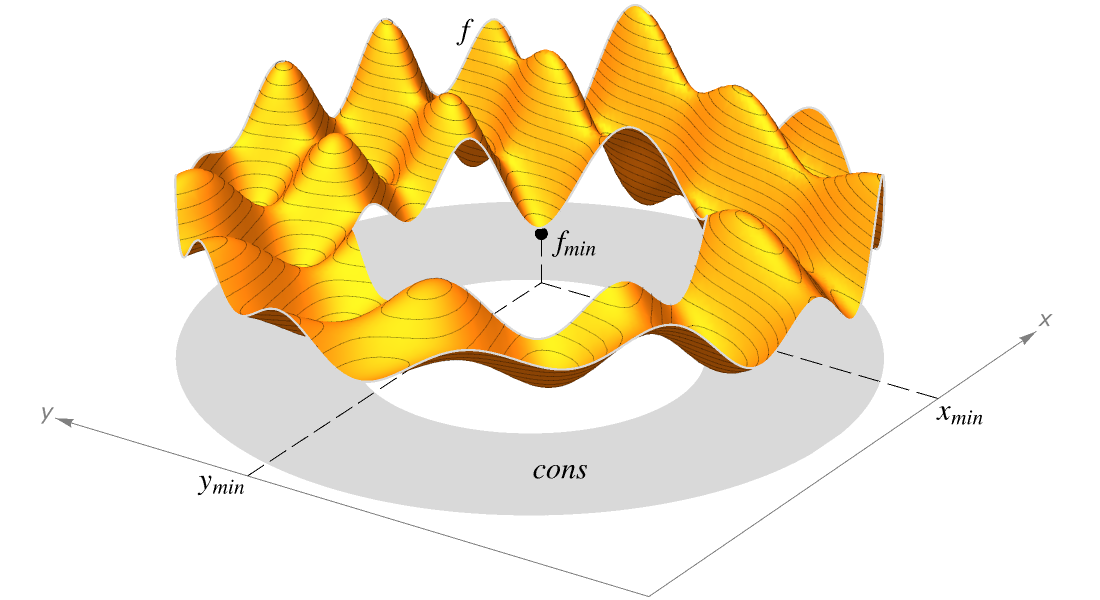
目的関数についての最適値を制約条件内で求めます.大域的最適値を求めるのには余分な労力がかかりますが,この労力は,多くの場合,経済,安全,効率等の理由でかちがあるものです.決定論的拡張,凸最適化,確率論的進化等のさまざまなメソッドが使えます.
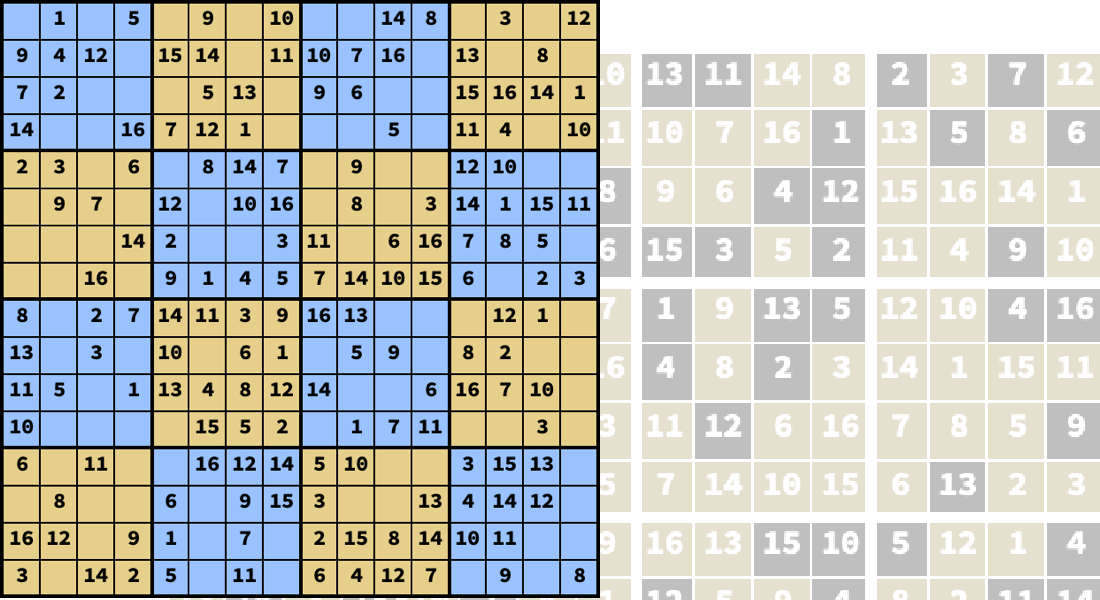
混合整数最適化
決定変数のいくつかが離散値あるいは整数値しか持たないような凸最適化問題を解きます.離散変数は,割当て,スケジューリング,経路選択等の問題でよく見られるものです.分枝限定法,切除平面法,外側近似法等を使って混合整数問題を効率的に解きます.
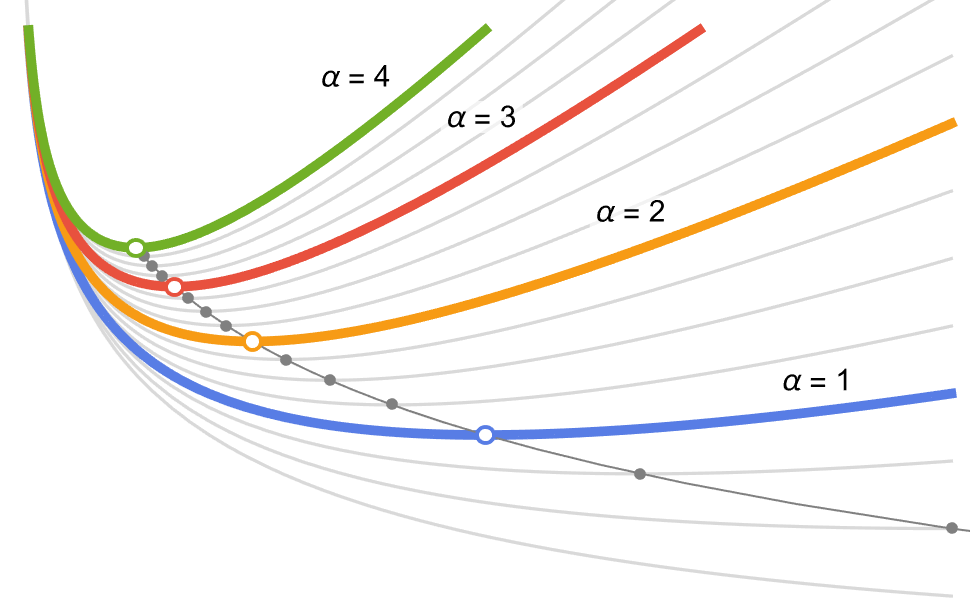
パラメトリック最適化
目的関数と制約条件でパラメータを使って一連の最適化問題を解きます.多くの解を効率的(パラメータスイープ)に求めたり,すべての値について安全な解(ロバスト最適化),乱数値について期待される解(確率的最適化),値の変化に対する感度(パラメトリック感度)を求めたりします.
記号最適化
最適化問題に対する厳密な大域解についての式を取得します.閉じた形の解は,検証され,再利用可能で,他の式と組み合せることができます.厳密な記号メソッドと近似数値メソッドに同じモデリング言語が使えます.

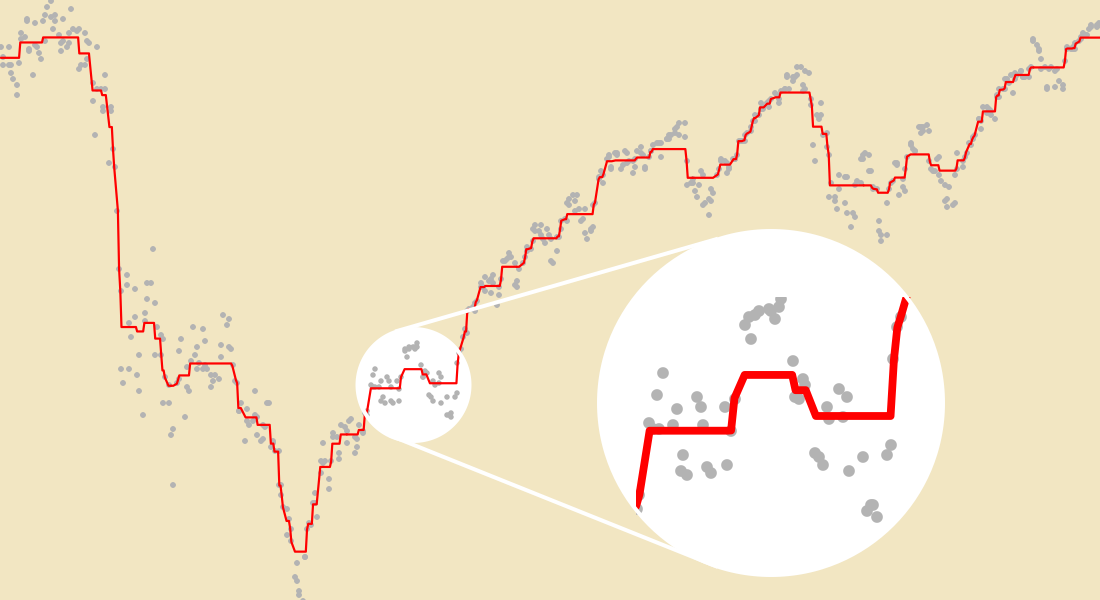
最適フィット
データ点の集合を最適にフィットさせるモデルパラメータを求めます.モデルのフィッティングはモデルとデータを関連付けるもので,他の値の推測を容易にします.最小二乗法,最小絶対偏差法,LASSO法,リッジ回帰法等の目的関数を利用する線形および非線形のフィッティングアルゴリズムを使います.
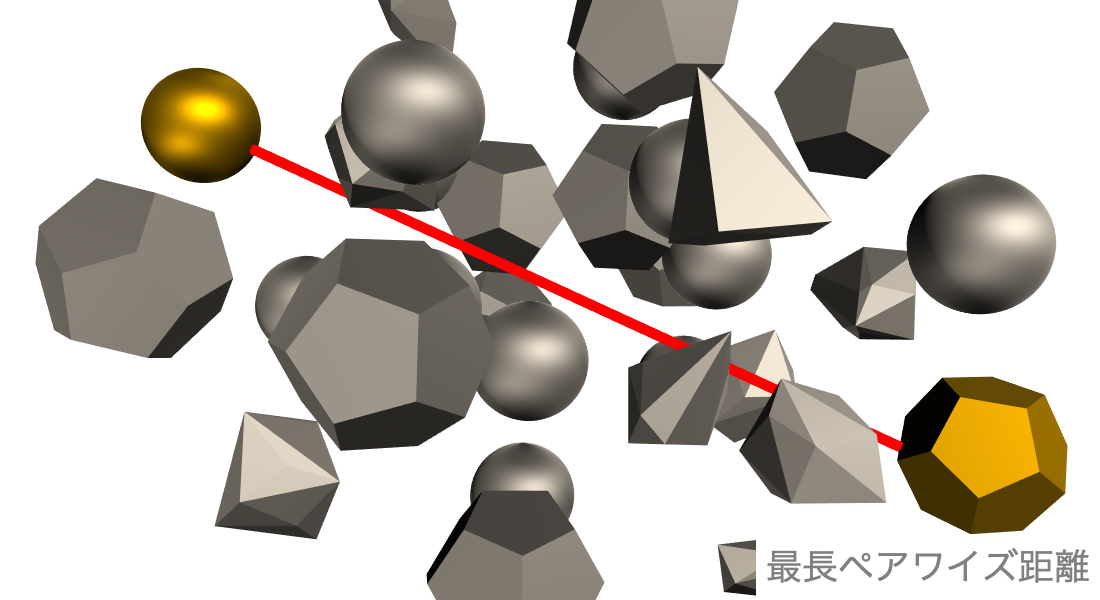
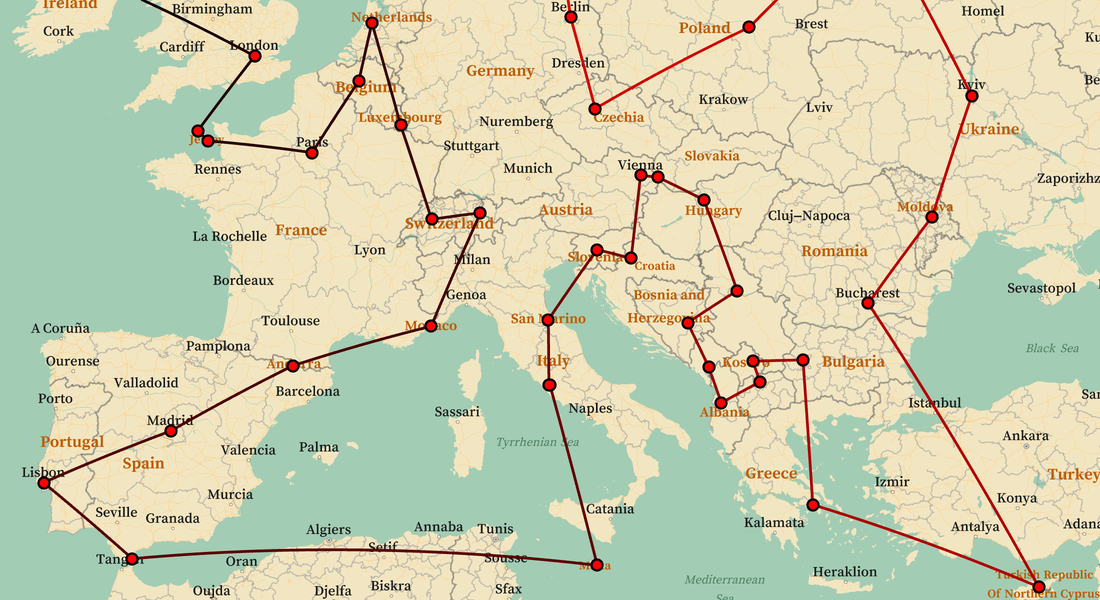
特殊目的の最適化
専用の関数を使って重要な最適化タスクを簡単にモデル化し効率的に解きます.直感的なインターフェースを使ってニューラルネットワークの訓練問題,巡回セールスマン問題,ナップサック問題を含む特別な最適化問題を解きます.
最適化のパートナー
Gurobi,MOSEK,FICO Xpressの商用ソルバが直接活用できます.大規模混合整数最適化にはクラスで最高のソルバが役立ちます.最適化関数はお客様がライセンスをお持ちのメソッドを自動的に使用します.

最適化に関するWolframドキュメント
Wolfram 最適化は,Wolfram言語に統合されています.全システムに計算の全分野を網羅する6,000個を超える組込み関数が含まれており,そのすべてが綿密に統合されているため,完全に一体となって作動します.


全領域とドキュメント