WolframOptimisationUn élément essentiel de
Wolfram Language
Modélisez, résolvez et analysez les conceptions graphiques.
Les fonctionnalités de Wolfram pour l’optimisation fournissent une palette complète d’outils pour trouver la meilleure conception graphique ou prendre la meilleure décision en fonction des contraintes. Elle est entièrement intégrée à l’apprentissage automatique, aux statistiques, aux données intégrées immédiatement calculables, et bien plus encore, le tout entièrement automatisé.
Modélisation de l’optimisation
Modélisez les objectifs et les contraintes à l’aide de fonctions mathématiques, d’inégalités et d’inclusion. Définissez des modèles compacts de haut niveau de manière naturelle avec des variables vectorielles, des inégalités vectorielles et des régions géométriques. Créez des modèles réutilisables en les construisant par programme à partir de données, de graphes et de tout autre objet.
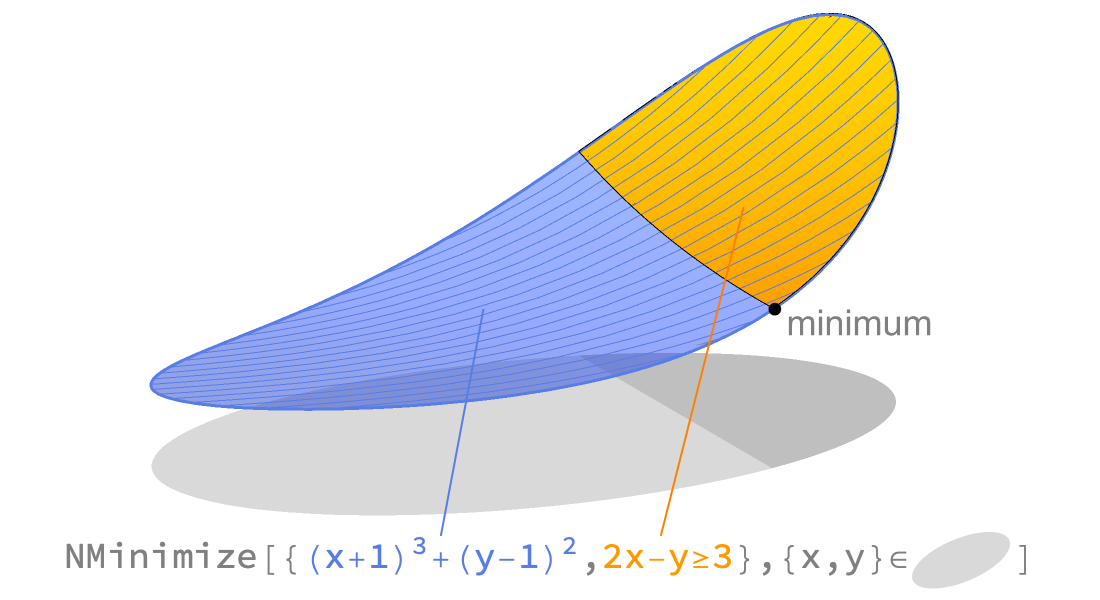
Optimisation linéaire et convexe
Résolvez les problèmes d’optimisation convexe à grande échelle avec des méthodes globales, rapides et fiables. L’optimisation convexe comprend des classes importantes telles que l’optimisation linéaire, quadratique, conique du second ordre, semi-définie et conique.
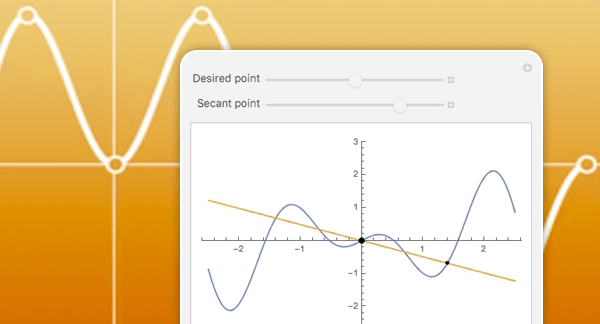
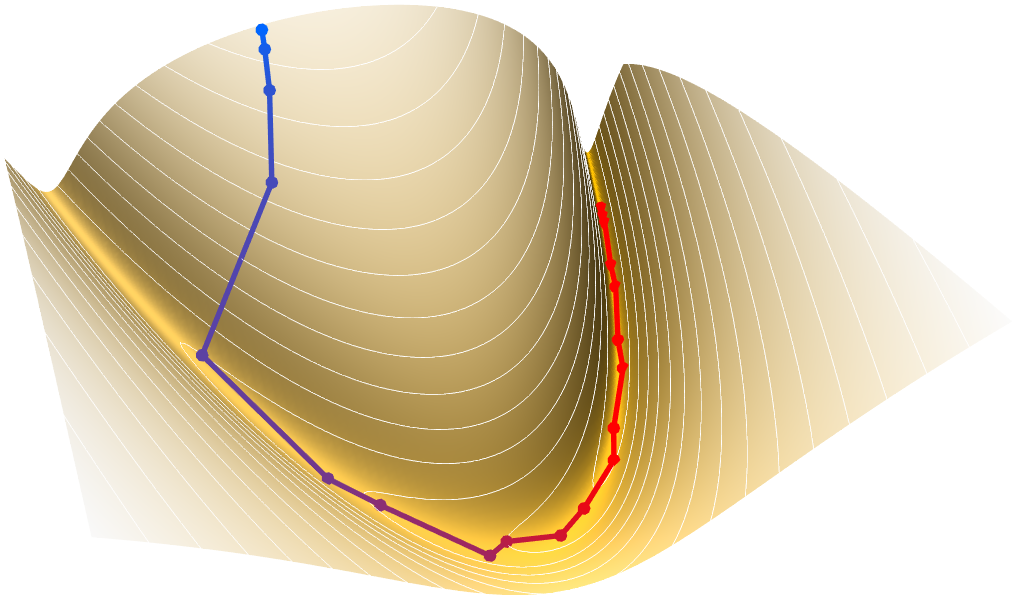
Optimisation locale
Trouvez un optimum local pour les problèmes d’optimisation avec ou sans contraintes. Les méthodes locales sont rapides et évolutives et sont souvent suffisantes. Elles peuvent aussi être utilisées pour créer des méthodes plus élaborées. Résolvez en utilisant une sélection automatisée de méthodes telles que la quasi Newton au point intérieur, ainsi que le calcul des dérivées et la compilation pour plus d’efficacité.
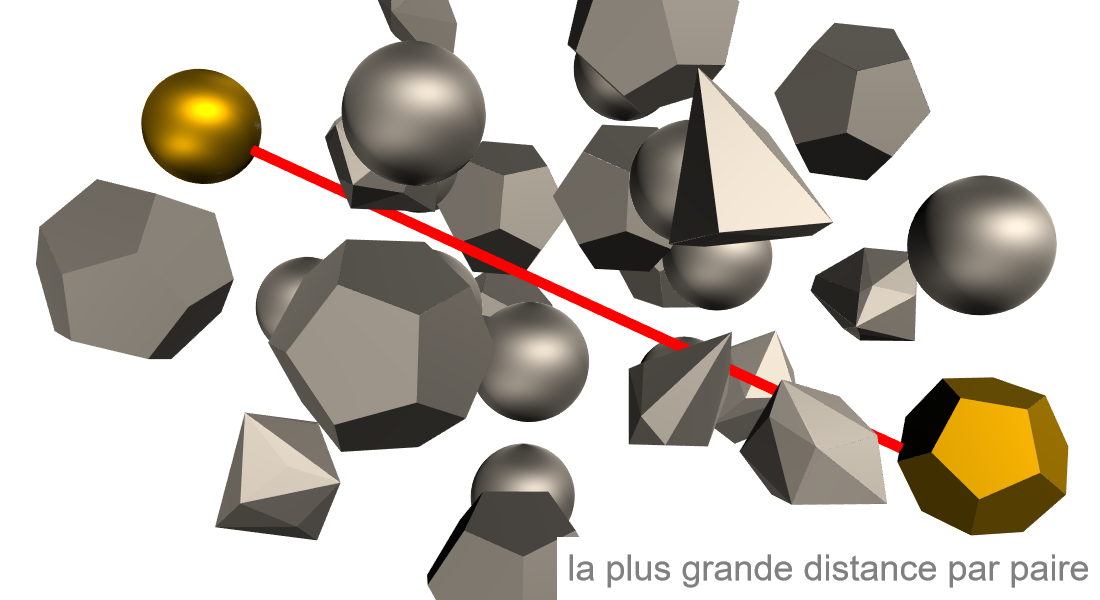
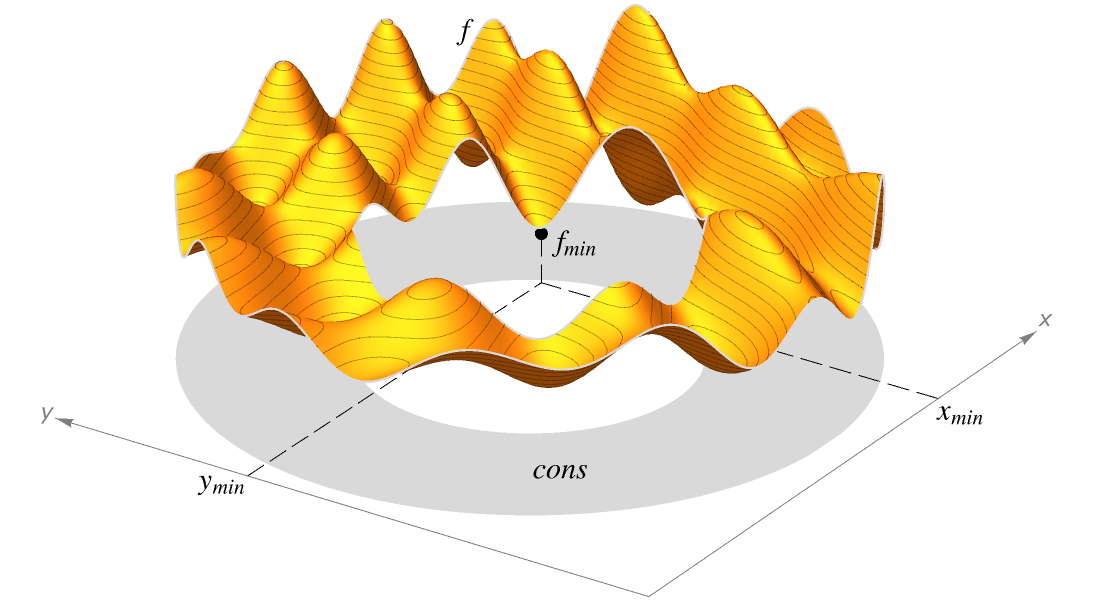
Optimisation globale
Cherchez la meilleure valeur possible pour un objectif dans le cadre de contraintes données. L’effort supplémentaire requis pour trouver un optimum global est souvent utile pour des raisons financières, de sécurité ou d’efficacité. Utilisez une grande variété de méthodes telles que les extensions déterministes de l’optimisation convexe et les méthodes évolutionnaires stochastiques.
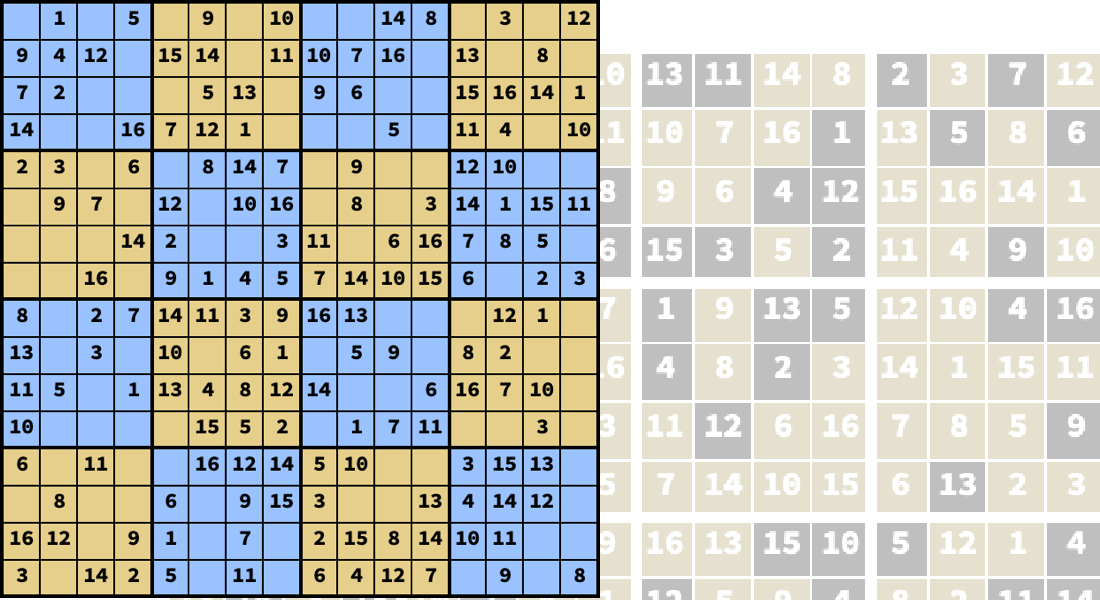
Optimisation en nombres entiers mixtes
Résolvez des problèmes d’optimisation convexes où certaines des variables de décision ne peuvent avoir que des valeurs discrètes ou entières. Les variables discrètes sont fréquentes dans les problèmes d’affectation, d’ordonnancement et de routage. Utilisez les méthodes de branchement et de limitation, de plan de coupe et d’approximation externe pour résoudre efficacement les problèmes à nombres entiers mixtes.
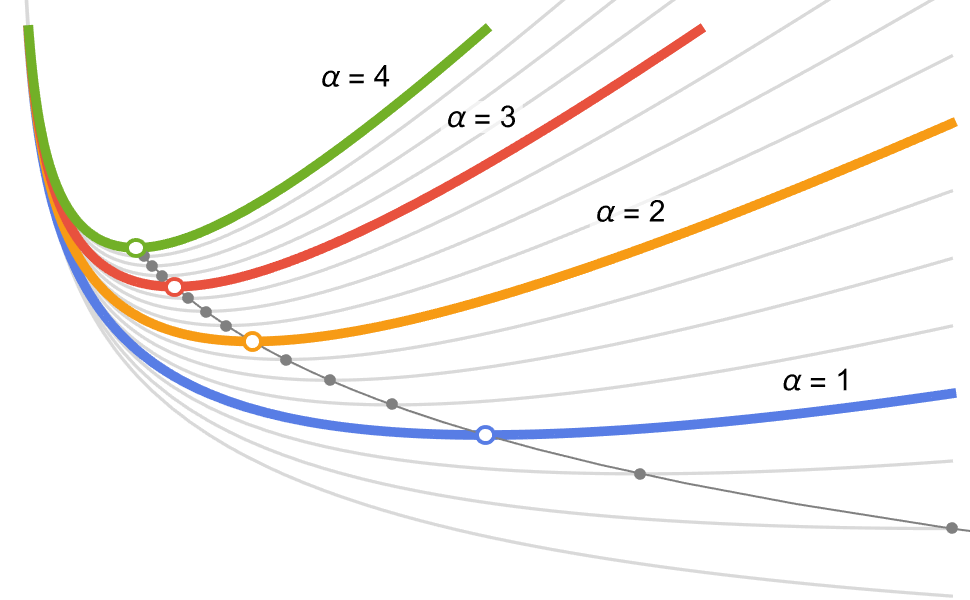
Optimisation paramétrique
Résolvez des familles de problèmes d’optimisation en utilisant des paramètres dans les objectifs et les contraintes. Trouvez de nombreuses solutions de manière efficace (balayage des paramètres), des solutions sûres pour toutes les valeurs (optimisation robuste), des solutions attendues pour des valeurs aléatoires (optimisation stochastique) ou la sensibilité aux changements de valeurs (sensibilité paramétrique).
Optimisation symbolique
Obtenez des formules pour des solutions globales exactes aux problèmes d’optimisation. Les solutions à forme fermée sont vérifiées, réutilisables et combinables avec d’autres formules. Utilisez le même langage de modélisation avec des méthodes symboliques exactes ou numériques approximatives.
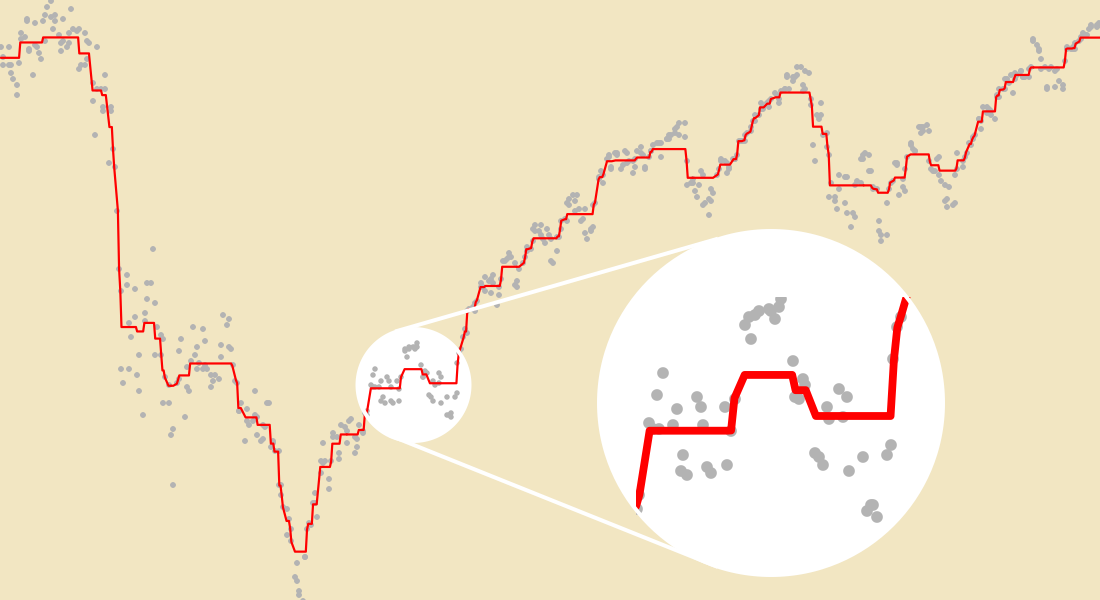
Ajustement optimal
Trouvez les paramètres d’un modèle qui correspondent le mieux à un ensemble de points de données. L’ajustement de modèle est la passerelle entre les modèles et les données, permettant de déduire facilement d’autres valeurs. Utilisez des algorithmes d’ajustement linéaires et non linéaires qui utilisent des objectifs tels que les moindres carrés, la plus petite déviation absolue, LASSO et la régression Ridge.
Optimisation à usage spécifique
Modélisez facilement et résolvez efficacement les tâches d’optimisation importantes à l’aide de fonctions dédiées. Utilisez des interfaces intuitives pour résoudre les problèmes de formation de réseaux neuronaux, de vendeur itinérant, de sac à dos et d’autres problèmes d’optimisation spéciaux.
Partenaires d’optimisation
Tirez immédiatement parti des solveurs commerciaux de Gurobi, MOSEK et FICO Xpress. Pour l’optimisation à grande échelle et l’optimisation en nombres entiers mixtes, les meilleurs solveurs de leur catégorie peuvent fournir un avantage nécessaire. Les fonctions d’optimisation peuvent utiliser automatiquement les méthodes pour lesquelles vous disposez d’une licence.
Documentation de Wolfram Optimisation
Wolfram Optimisation fait partie intégrante de Wolfram Language. Le système complet contient plus de 6000 fonctions intégrées couvrant tous les domaines du calcul, toutes soigneusement intégrées pour fonctionner parfaitement ensemble.
Champ d'application et documentation
Guide
Guide
GuideCours d'introduction
Démarrer avec Wolfram Optimisation
Accéder à Wolfram Language via Wolfram|One ou Mathematica
