Biologists have considerable interest in simple pieces that combine into a greater whole. Ants form a sophisticated society. A school of fish turns sharply in unison. Pacemaker cells synchronize to a heartbeat while billions of neurons conjure a thought.

The aquatic colony Hydractiniid Hydroid is composed of connected polyps, cylindrical organisms capable of absorbing food from the environment and digesting it. Though a polyp responds only to its immediate surroundings and can interact with others only through a connecting tube for sharing fluid, a colony of hundreds of individual polyps is capable of integrated environmental responses. Nutrients are distributed to the polyps that need them the most. Colonies develop with dramatically different structures depending on the availability of food. (See an animation of a contracting polyp.)

To more easily simulate colonies with large numbers of polyps, Professor Leo Buss of Yale University wanted to know if each polyp could be represented as a simple non-linear oscillator. To assist him, Rimas Surna, a specialist in advanced imaging techniques, developed a process to convert videos of individual polyps into a digital representation that could be studied in three dimensions with the aid of Mathematica.

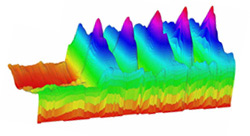
Using the graph below, the shape of the polyp at any time during its oscillations can be seen in the cross sections at the tops of the ridges, the bottoms of the valleys, or for time in between. While the oscillations on the side connected to the communal fluid of the colony vary considerably, the big oscillatory peaks in the middle of the polyp remain remarkably stable despite the external influences. This behavior suggests analogies to non-linear systems such as certain types of neurons whose multiple firings depend only on initial conditions.

Are comparisons between otherwise disparate phenomena useful, or are their similarities merely superficial? With the aid of advanced visualization software such as Mathematica, each new experiment has the potential to provide convincing evidence or inspire unexpected connections.

Related Stories